ВЗАИМОДЕЙСТВИЕ ПРОДОЛЬНОГО И БОКОВОГО ДВИЖЕНИЯ САМОЛЕТА ПРИ МАНЁВРЕ*

В § 18.1 показано, что при маневре с постоянной угловой скоростью крена начальную фазу пространственного возмущенного движения самолета можно описать системой четырех линейных диф­ференциальных уравнений с постоянными коэффициентами. Следо­вательно, устойчивость такого возмущенного движения можно исследовать теми же методами, которые применялись ранее при исследовании устойчивости изолированного продольного и изолиро­ванного бокового возмущенного движения. Характеристическое уравнение системы дифференциальных уравнений пространствен­ного возмущенного движения. будет иметь тот же самый вид

Я4 + asKs + ай%й ч — + а0 = 0, (18.15)

но коэффициенты этого уравнения будут выражаться, конечно, иначе. Они будут определяться характеристиками и продольного, и бокового каналов.

Условия устойчивого пространственного движения будут выра­жаться известными неравенствами R — а^а3 — а — а|а0 > 0; as > 0, а, > 0; аг > 0; Оу > 0, последнее из которых является условием апериодической устойчивости.

Расчеты устойчивости пространственного движения показывают, что если выполняется это последнее условие, выполняются и все
предыдущие. Поэтому остановимся подробнее на Выражении для коэффициента а0. Получим его, раскрывая определитель системы

(18.13) . Свободный^член характеристического уравнения (18.15) имеет следующий вид:

а0 = — (Bui +Ж“ + МггТ°) (Ad +ЖР — ЖУЧ?) +

+ d (BZ* +ЖУ) (ЖУ — А? а). (18.16)

Как видно из выражения (18.16), на апериодическую устой­чивость движения самолета с угловой скоростью крена влияет ве­личина этой скорости. Если она мала (сож->-0), неравенство а0 > О удовлетворяется при условиях

(Ж? +MzzYa) <0; (18.17)

(ЖР-Ж>1Р)<0. (18.J8)

Это означает, что самолет устойчив в пространственном движении при наличии продольной статической устойчивости по перегрузке — неравенство (18.17) и путевой (флюгерной) статической устойчи­вости — неравенство (18.18).

При больших скоростях крена положение меняется. Чтобы с большей наглядностью выявить особенности апериодической устойчивости пространственного движения самолета при больших угловых скоростях крена, выделим основную часть в выражении свободного члена характеристического уравнения, отбросив второе менее существенное слагаемое. Тогда приближенно’ Оо будет иметь следующий вид:

Оо = — (Bd + Мг + ЖгУа) (а4 + Щ — МуЧ?). (18.19)

Из полученного выражения видно, что несмотря на наличие у самолета продольной статической устойчивости по перегрузке и путевой (флюгерной) статической устойчивости, свободный член а0 при увеличении угловой скорости крена до некоторого критического значения меняет знак с положительного на отрицательный. Это значение угловой скорости называют первой критической скоростью крена. При достижении такой скорости самолет при маневре выхо­дит на границу апериодической устойчивости, а при небольшом превышении ее становится апериодически неустойчивым.

В первом приближении моменту потери устойчивости соответ­ствует изменение знака одного из множителей в выражении (18.19). При дальнейшем увеличении скорости крена она достигает такой величины, когда и второй множитель меняет знак — это вторая критическая скорость. С превышением ее самолет становится снова устойчивым. Наиболее типичная зависимость свободного члена ха­рактеристического уравнения от угловой скорости крена показана на рис. 18.4, а. Она характеризуется наличием двух критических скоростей, приближенное значение которых можно получить, при-

Рис. 18.4. Типовые зависимости а0 == Рис. 18.5. Границы абсолютной устой — = / (<й^) чивости пространственного движения равнивая нулю каждый из множителей выражения (18.19). Вели­чина одной из этих скоростей определяется, как видно, характери­стиками продольной устойчивости, другой — характеристиками бо­ковой устойчивости. Обозначив критические скорости соответственно через С0а И СОр, получим их приближенные значения

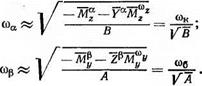
(18.20)

(18.21)

Как видно из формул (18.20) и (18.21) критические скорости крена зависят от частот свободных колебаний в изолированном продольном и изолированном боковом движении, а также от соот­ношения между осевыми моментами инерции самолета. Меньшая из этих скоростей — первая критическая скорость — может опреде­ляться как характеристиками продольной, так и характеристиками боковой устойчивости.

Могут иметь место случаи, когда критические скорости <ва и ©р равны. Тогда зависимость свободного члена характеристического уравнения от скорости крена будет иметь вид, изображенный на рис. 18.4,6. Если строить зависимость а0 = / (ю*) с’помощью не приближенного, а точного выражения для а0 [формула (18.16)], то можно получить и иной [характер этой зависимости (см. рис. 18.4, в). Это будет случай, когда самолет не теряет устойчи­вости в пространственном (движении при любых значениях ско­рости крена, т. е. обладает абсолютной устойчивостью. Так как из всего множества величин, входящих в выражение (18.16) и влия­ющих на устойчивость самолета, с наименьшими трудностями под­даются изменению^характеристики статической устойчивости, най­дем границу абсолютной устойчивости ца плоскости т“, т^.

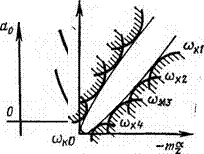
Для этого дадим конкретные числовые значения всем величинам в формуле свободного члена (18.16), кроме т“ и т®. Варьируя зна­
чения угловой скорости крена, получим семейство гипербол, изобра­женное на рис. 18.5. Огибающая этого семейства — парабола. Она’и будет искомой границей устойчивости. Внутри этой границы находится область абсолютной устойчивости пространственного движения, т. е. такие значения тл“ и ту, при которых самолет устой­чив в пространственном движении при любых значениях угловой скорости крена. Анализ области устойчивости показывает, что самолет, обладающий абсолютной устойчивостью при некоторых значениях т“, т^, будет приближаться к границе устойчивости и может выйти за ее пределы, если будет увеличиваться разница между этими значениями. Полагая, например, m“ = const, ви­дим, что при чрезмерном увеличении и уменьшении флюгерной статической устойчивости изображающая точка на плоскости тл“, «4 выходит за пределы зоны устойчивости. Если построить границы устойчивости при различных значениях продольного и путевого демпфирования, можно убедиться, что с увеличением демпфирую­щих моментов область устойчивости увеличивается.

Из приведенных ранее данных следует, что проблема сохранения устойчивости при маневре для современных самолетов стала акту­альной и достаточно сложной по ряду причин. Это и изменение инерционных характеристик современных самолетов вследствие их специфической геометрии. Это и изменение аэродинамических ха­рактеристик в связи с широким диапазоном скоростей и влиянием сжимаемости на около — и сверхзвуковых скоростях полета. Как известно, вследствие влияния сжимаемости продольная статическая устойчивость самолета на больших скоростях растет, тогда как флюгерная устойчивость падает. Как видно из рис. 18.5, различные уровни продольной и флюгерной устойчивости не обеспечивают устойчивости пространственного движения с угловой скоростью крена. Неизбежна потеря устойчивости^ при ^скоростях,* больших первой критической и меньших второй критической скорости. Ма­лая продольная статическая устойчивость на дозвуковых скоростях и малая флюгерная статическая устойчивость на сверхзвуковых скоростях снижают первую критическую скорость до величин, достижимых при реальных маневрах самолета. Избежать^этого рациональной компоновкой удается далеко не всегда.

Обеспечение устойчивости пространственного движения совре­менных сверхзвуковых самолетов достигается, в основном, вслед­ствие применения автоматики, которая одновременно служит и для улучшения иных характеристик самолета. Так нашедшие широкое применение автоматы демпфирования, автоматы устойчивости на­ряду с улучшением устойчивости и управляемости в продольном и боковом движении позволяют обеспечить в рабочих диапазонах режимов полета и устойчивость пространственного движения при маневре.